- AVEDEV 函数
- AVERAGE 函数
- AVERAGEA 函数
- AVERAGEIF 函数
- AVERAGEIFS 函数
- BETA.DIST 函数
- BETA.INV 函数
- BINOM.DIST 函数
- BINOM.DIST.RANGE 函数
- BINOM.INV 函数
- CHISQ.DIST 函数
- CHISQ.DIST.RT 函数
- CHISQ.INV 函数
- CHISQ.INV.RT 函数
- CHISQ.TEST 函数
- CONFIDENCE.NORM 函数
- CONFIDENCE.T 函数
- CORREL 函数
- COUNT 函数
- COUNTA 函数
- COUNTBLANK 函数
- COUNTIF 函数
- COUNTIFS 函数
- COVARIANCE.P 函数
- COVARIANCE.S 函数
- DEVSQ 函数
- EXPON.DIST 函数
- F.DIST 函数
- F.DIST.RT 函数
- F.INV 函数
- F.INV.RT 函数
- FINV 函数
- FISHER 函数
- FISHERINV 函数
- FORECAST 函数
- FORECAST.ETS 函数
- FORECAST.ETS.CONFINT 函数
- FORECAST.ETS.SEASONALITY 函数
- FORECAST.ETS.STAT 函数
- FORECAST.LINEAR 函数
- FREQUENCY 函数
- F.TEST 函数
- GAMMA 函数
- GAMMA.DIST 函数
- GAMMA.INV 函数
- GAMMALN 函数
- GAMMALN.PRECISE 函数
- GAUSS 函数
- GEOMEAN 函数
- GROWTH 函数
- HARMEAN 函数
- HYPGEOM.DIST 函数
- INTERCEPT 函数
- KURT 函数
- LARGE 函数
- LINEST 函数
- LOGEST 函数
- LOGNORM.DIST 函数
- LOGNORM.INV 函数
- MAX 函数
- MAXA 函数
- MAXIFS 函数
- MEDIAN 函数
- MIN 函数
- MINIFS 函数
- MINA 函数
- MODE.MULT 函数
- MODE.SNGL 函数
- NEGBINOM.DIST 函数
- NORM.DIST 函数
- NORMINV 函数
- NORM.S.DIST 函数
- NORM.S.INV 函数
- PEARSON 函数
- PERCENTILE.EXC 函数
- PERCENTILE.INC 函数
- PERCENTRANK.EXC 函数
- PERCENTRANK.INC 函数
- PERMUT 函数
- PERMUTATIONA 函数
- PHI 函数
- POISSON.DIST 函数
- PROB 函数
- QUARTILE.EXC 函数
- QUARTILE.INC 函数
- RANK.AVG 函数
- RANK.EQ 函数
- RSQ 函数
- SKEW 函数
- SKEW.P 函数
- SLOPE 函数
- SMALL 函数
- STANDARDIZE 函数
- STDEV.P 函数
- STDEV.S 函数
- STDEVA 函数
- STDEVPA 函数
- STEYX 函数
- T.DIST 函数
- T.DIST.2T 函数
- T.DIST.RT 函数
- T.INV 函数
- T.INV.2T 函数
- TREND 函数
- TRIMMEAN 函数
- T.TEST 函数
- VAR.P 函数
- VAR.S 函数
- VARA 函数
- VARPA 函数
- WEIBULL.DIST 函数
- Z.TEST 函数
LINEST 函数
本文介绍 Microsoft Excel 中 LINEST 函数的公式语法和用法。
说明
LINEST 函数可通过使用最小二乘法计算与现有数据最佳拟合的直线,来计算某直线的统计值,然后返回描述此直线的数组。 也可以将 LINEST 与其他函数结合使用来计算未知参数中其他类型的线性模型的统计值,包括多项式、对数、指数和幂级数。 因为此函数返回数值数组,所以它必须以数组公式的形式输入。 请按照本文中的示例使用此函数。
直线的公式为:
y = mx + b
- 或 -
y = m1x1 + m2x2 + ... + b
如果有多个区域的 x 值,其中因变量 y 值是自变量 x 值的函数。 m 值是与每个 x 值相对应的系数,b 为常量。 注意,y、x 和 m 可以是向量。 LINEST 函数返回的数组为 {mn,mn-1,...,m1,b}。 LINEST 函数还可返回附加回归统计值。
语法
LINEST(known_y's, [known_x's], [const], [stats])
LINEST 函数语法具有下列参数:
语法
-
Known_y's 必需。 关系表达式 y = mx + b 中已知的 y 值集合。
-
如果 known_y's 对应的单元格区域在单独一列中,则 known_x's 的每一列被视为一个独立的变量。
-
如果 known_y's 对应的单元格区域在单独一行中,则 known_x's 的每一行被视为一个独立的变量。
-
-
Known_x's 可选。 关系表达式 y = mx + b 中已知的 x 值集合。
-
known_x's 对应的单元格区域可以包含一组或多组变量。 如果仅使用一个变量,那么只要 known_x's 和 known_y's 具有相同的维数,则它们可以是任何形状的区域。 如果用到多个变量,则 known_y's 必须为向量(即必须为一行或一列)。
-
如果省略 known_x's,则假设该数组为 {1,2,3,...},其大小与 known_y's 相同。
-
-
const 可选。 一个逻辑值,用于指定是否将常量 b 强制设为 0。
-
如果 const 为 TRUE 或省略,b 将按正常计算。
-
如果 const 为 FALSE,b 将被设为 0,并同时调整 m 值使 y = mx。
-
-
stats 可选。 一个逻辑值,用于指定是否返回附加回归统计值。
-
如果 stats 为 TRUE,则 LINEST 函数返回附加回归统计值,这时返回的数组为 {mn,mn-1,...,m1,b;sen,sen-1,...,se1,seb;r2,sey;F,df;ssreg,ssresid}。
-
如果 stats 为 FALSE 或省略,则函数 LINEST 只返回系数 m 和常量 b。
附加回归统计值如下:
-
|
统计值 |
说明 |
|
se1,se2,...,sen |
系数 m1,m2,...,mn 的标准误差值。 |
|
seb |
常量 b 的标准误差值(当 const 为 FALSE 时,seb = #N/A)。 |
|
r2 |
判定系数。 y 的估计值与实际值之比,范围在 0 到 1 之间。 如果为 1,则样本 有很好的相关性,y 的估计值与实际值之间没有差别。 相反,如果判定系数为 0,则回归公式不能用来预测 y 值。 有关如何计算 r2 的信息,请参阅本主题下文中的“说明”。 |
|
sey |
Y 估计值的标准误差。 |
|
F |
F 统计或 F 观察值。 使用 F 统计可以判断因变量和自变量之间是否偶尔发生过可观察到的关系。 |
|
df |
自由度。 用于在统计表上查找 F 临界值。 将从表中查得的值与 LINEST 函数返回的 F 统计值进行比较可确定模型的置信区间。 有关如何计算 df 的信息,请参阅本主题下文中的“说明”。 示例 4 说明了 F 和 df 的用法。 |
|
ssreg |
回归平方和。 |
|
ssresid |
残差平方和。 有关如何计算 ssreg 和 ssresid 的信息,请参阅本主题下文中的“说明”。 |
下面的图示显示了附加回归统计值返回的顺序。

备注
-
可以使用斜率和 y 轴截距描述任何直线:
斜率 (m): 通常记为 m,如果需要计算斜率,则选取直线上的两点,(x1,y1) 和 (x2,y2);斜率等于 (y2 - y1)/(x2 - x1)。
Y 轴截距 (b): 通常记为 b,直线的 y 轴的截距为直线通过 y 轴时与 y 轴交点的数值。
直线的公式为 y = mx + b。 如果知道了 m 和 b 的值,将 y 或 x 的值代入公式就可计算出直线上的任意一点。 还可以使用 TREND 函数。
-
当只有一个自变量 x 时,可直接利用下面公式得到斜率和 y 轴截距值:
斜率: =INDEX(LINEST(known_y's,known_x's),1)
Y 轴截距: =INDEX(LINEST(known_y's,known_x's),2)
-
数据的离散程度决定了 LINEST 函数计算的直线的精确度。 数据越接近线性,LINEST 模型就越精确。 LINEST 函数使用最小二乘法来判定数据的最佳拟合。 当只有一个自变量 x 时,m 和 b 是根据下面的公式计算出的:
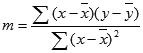
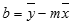
其中,x 和 y 是样本平均值;即,x = AVERAGE(known x's) 且 y = AVERAGE(known_y's)。
-
直线和曲线拟合函数 LINEST 和 LOGEST 可用来计算与给定数据拟合程度最高的直线或指数曲线, 但需要判断两者中哪一个与数据拟合程度最高。 可以用函数 TREND(known_y's,known_x's) 来计算直线,或用函数 GROWTH(known_y's, known_x's) 来计算指数曲线。 这些不带 new_x's 参数的函数可在实际数据点上根据直线或曲线来返回 y 预测值的数组, 然后可以将预测值与实际值进行比较。 可能需要用图表方式来直观地比较二者。
-
回归分析时,Excel 会计算每一点的 y 的估计值和实际值的平方差。 这些平方差之和称为残差平方和 (ssresid)。 然后 Excel 会计算总平方和 (sstotal)。 当参数 const = TRUE 或被省略时,总平方和是 y 的实际值和平均值的平方差之和。 当参数 const = FALSE 时,总平方和是 y 的实际值的平方和(不需要从每个 y 值中减去平均值)。 回归平方和 (ssreg) 可通过公式 ssreg = sstotal - ssresid 计算出来。 残差平方和与总平方和的比值越小,判定系数 r2 的值就越大,r2 是用来判断从回归分析求得的公式是否足以说明变量之间关系的指示器。 r2 = ssreg/sstotal。
-
在某些情况下,一个或多个 X 列可能没有出现在其他 X 列中的附加预测值(假设 Y's 和 X's 位于列中)。 换句话说,删除一个或多个 X 列可能会得到同样精度的 y 预测值。 在这种情况下,应从回归模型中省略这些多余的 X 列。 这种现象被称为“共线”,因为任何多余的 X 列都可被表示为多个非多余 X 列的和。 LINEST 函数会检查是否存在共线,并在识别出多余的 X 列之后从回归模型中删除所有这些列。 由于包含 0 系数以及 0 se 数值,因此已删除的 X 列能在 LINEST 输出中被识别出来。 如果一个或多个多余的列被删除,则将影响 df,原因是 df 取决于实际用于预测目的的 X 列的数量。 有关计算 df 的详细信息,请参阅示例 4。 如果由于删除多余的 X 列而更改了 df,则也会影响 sey 和 F 的值。 实际上,出现共线的情况应该相对很少。 但是,如果某些 X 列仅包含 0 和 1 数值作为实验中的对象是否属于特定组成员的指示器,则很可能引起共线。 如果 const = TRUE 或被省略,则 LINEST 函数可有效地插入所有 1 数值的其他 X 列以便为截距建立模型。 如果在一列中,1 对应于每个男性对象,0 对应于女性对象;而在另一列中,1 对应于每个女性对象,0 对应于男性对象,那么后一列就是多余的,因为其中的项可通过从所有 1 值的另一列(通过 LINEST 函数添加)中减去“男性指示器”列中的项来获得。
-
在没有 X 列因共线而被从模型中删除时,请用以下方法计算 df 的值:如果 known_x’s 有 k 列且 const = TRUE 或被省略,那么 df = n – k – 1。 如果 const = FALSE,那么 df = n - k。 在这两种情况下,每次由于共线而删除一个 X 列都会使 df 的值加 1。
-
对于返回结果为数组的公式,必须以数组公式的形式输入。
注意: 在 Excel Online 中,不能创建数组公式。
-
当输入一个数组常量(如 known_x's)作为参数时,请使用逗号分隔同一行中的各值,使用分号分隔各行。 分隔符可能会因区域设置的不同而有所不同。
-
注意,如果 y 的回归分析预测值超出了用来计算公式的 y 值的范围,它们可能是无效的。
-
LINEST 函数中使用的下层算法与 SLOPE 和 INTERCEPT 函数中使用的下层算法不同。 当数据未定且共线时,这些算法之间的差异会导致不同的结果。 例如,如果参数 known_y's 的数据点为 0,参数 known_x's 的数据点为 1:
-
LINEST 会返回值 0。 LINEST 函数的算法用来返回共线数据的合理结果,在这种情况下至少可找到一个答案。
-
SLOPE 和 INTERCEPT 返回 错误 #DIV/0!。 SLOPE 和 INTERCEPT 函数的算法只用来查找一个答案,在这种情况下可能有多个答案。
-
-
除了使用 LOGEST 计算其他回归分析类型的统计值外,还可以使用 LINEST 计算其他回归分析类型的范围,方法是将 x 和 y 变量的函数作为 LINEST 的 x 和 y 系列输入。 例如,下面的公式:
=LINEST(yvalues, xvalues^COLUMN($A:$C))
将在您使用 y 值的单个列和 x 值的单个列计算下面的方程式的近似立方(多项式次数 3)值时运行:
y = m1*x + m2*x^2 + m3*x^3 + b
可以调整此公式以计算其他类型的回归,但是在某些情况下,需要调整输出值和其他统计值。
-
LINEST 函数返回的 F 检验值与 FTEST 函数返回的 F 检验值不同。 LINEST 返回 F 统计值,而 FTEST 返回概率。
示例
示例 1 - 斜率和 Y 轴截距
复制下表中的示例数据,然后将其粘贴进新的 Excel 工作表的 A1 单元格中。 要使公式显示结果,请选中它们,按 F2,然后按 Enter。 如果需要,可调整列宽以查看所有数据。
|
已知 y |
已知 x |
|
1 |
0 |
|
9 |
4 |
|
5 |
2 |
|
7 |
3 |
|
结果(斜率) |
结果(Y 轴截距) |
|
2 |
1 |
|
公式(单元格 A7:B7 中的数组公式) |
|
|
=LINEST(A2:A5,B2:B5,,FALSE) |
示例 2 - 简单线性回归
复制下表中的示例数据,然后将其粘贴进新的 Excel 工作表的 A1 单元格中。 要使公式显示结果,请选中它们,按 F2,然后按 Enter。 如果需要,可调整列宽以查看所有数据。
|
月份 |
销售额 |
|
1 |
¥31,000 |
|
2 |
¥45,000 |
|
3 |
¥44,000 |
|
4 |
¥54,000 |
|
5 |
¥75,000 |
|
6 |
¥81,000 |
|
公式 |
结果 |
|
=SUM(LINEST(B1:B6, A1:A6)*{9,1}) |
¥110,000 |
|
基于 1 月到 6 月的销售额,估算第 9 个月的销售额。 |
示例 3 - 多重线性回归
复制下表中的示例数据,然后将其粘贴进新的 Excel 工作表的 A1 单元格中。 要使公式显示结果,请选中它们,按 F2,然后按 Enter。 如果需要,可调整列宽以查看所有数据。
|
底层面积 (x1) |
办公室的个数 (x2) |
入口个数 (x3) |
办公楼的使用年数 (x4) |
办公楼的评估值 (y) |
|
2310 |
2 |
2 |
20 |
¥14,200,00 |
|
2333 |
2 |
2 |
12 |
¥14,400,00 |
|
2356 |
3 |
1.5 |
33 |
¥15,100,00 |
|
2379 |
3 |
2 |
43 |
¥150,000,00 |
|
2402 |
2 |
3 |
53 |
¥13,900,00 |
|
2425 |
4 |
2 |
23 |
¥16,900,00 |
|
2448 |
2 |
1.5 |
99 |
¥12,600,00 |
|
2471 |
2 |
2 |
34 |
¥14,290,00 |
|
2494 |
3 |
3 |
23 |
¥16,300,00 |
|
2517 |
4 |
4 |
55 |
¥16,900,00 |
|
2540 |
2 |
3 |
22 |
¥14,900,00 |
|
-234.2371645 |
||||
|
13.26801148 |
||||
|
0.996747993 |
||||
|
459.7536742 |
||||
|
1732393319 |
||||
|
公式(A14:A18 中输入的数组公式) |
||||
|
=LINEST(E2:E12,A2:D12,TRUE,TRUE) |
示例 4 - 使用 F 和 r2 统计值
在上例中,判定系数 r2 为 0.99675(函数 LINEST 的输出单元格 A17 中的值),表明自变量与销售价格之间存在很强的相关性。 可以通过 F 统计值来确定具有如此高的 r2 值的结果偶然发生的可能性。
假设事实上在变量间不存在相关性,但选用 11 个办公楼作为小样本进行统计分析却导致很强的相关性。 术语“Alpha”表示得出这样的相关性结论错误的概率。
LINEST 函数输出中的 F 和 df 值可被用于评估偶然出现较高 F 值的可能性。 F 可与发布的 F 分布表中的值进行比较,或者 Excel 中的 FDIST 函数可被用于计算偶然出现较高 F 值的概率。 适当的 F 分布具有 v1 和 v2 自由度。 如果 n 是数据点的个数且 const = TRUE 或被省略,那么 v1 = n – df – 1 且 v2 = df。 (如果 const = FALSE,那么 v1 = n – df 且 v2 = df。)语法为 FDIST (F,v1,v2) 的 FDIST 函数 将返回偶然出现较高 F 值的概率。 在本例中,df = 6(单元格 B18)且 F = 459.753674(单元格 A18)。
假设 Alpha 值为 0.05,v1 = 11 – 6 – 1 = 4 且 v2 = 6,那么 F 的临界值为 4.53。 由于 F = 459.753674 远大于 4.53,所以偶然出现高 F 值的可能性非常低。 (因为,在 Alpha = 0.05 的情况下,当 F 超过临界值 4.53 时,known_y’s 和 known_x’s 之间没有关系这一假设不成立。)使用 Excel 中的 FDIST 函数可获得偶然出现高 F 值的概率。 例如,FDIST(459.753674, 4, 6) = 1.37E-7,是一个极小的概率。 于是可以断定,无论通过在表中查找 F 的临界值,还是使用 FDIST 函数,回归公式都可用于预测该区域中的办公楼的评估价值。 请注意,使用在上一段中计算出的 v1 和 v2 的正确值是非常关键的。
示例 5 - 计算 t 统计值
另一个假设测试可以判定每个斜率系数是否可以用来估算示例 3 中的办公楼的评估价值。 例如,要测试年龄系数的统计显著性水平,以 13.268(单元格 A15 中年龄系数的估计标准误差)除 -234.24(年龄斜率系数)。 下面是 t 观察值:
t = m4 ÷ se4 = -234.24 ÷ 13.268 = -17.7
如果 t 的绝对值足够大,那么可以断定斜率系数可用来估算示例 3 中的办公楼的评估价值。 下表显示了 4 个 t 观察值的绝对值。
如果查阅统计手册里的表,将会发现:双尾、自由度为 6、Alpha = 0.05 的 t 临界值为 2.447。 该临界值还可使用 Excel 中的 TINV 函数计算。 TINV(0.05,6) = 2.447。 既然 t 的绝对值为 17.7,大于 2.447,则办公楼的使用年数对于估算办公楼的评估价值来说是一个重要变量。 用同样方法,可以测试其他每个自变量的统计显著性水平。 以下是每个自变量的 t 观察值。
|
变量 |
t 观察值 |
|
底层面积 |
5.1 |
|
办公室的个数 |
31.3 |
|
入口个数 |
4.8 |
|
使用年数 |
17.7 |
这些值的绝对值都大于 2.447;因此,回归公式的所有变量都可用来估算此区域内的办公楼的评估价值。